Null hypothesis testing, estimation, and prediction: The prior predictive paradox

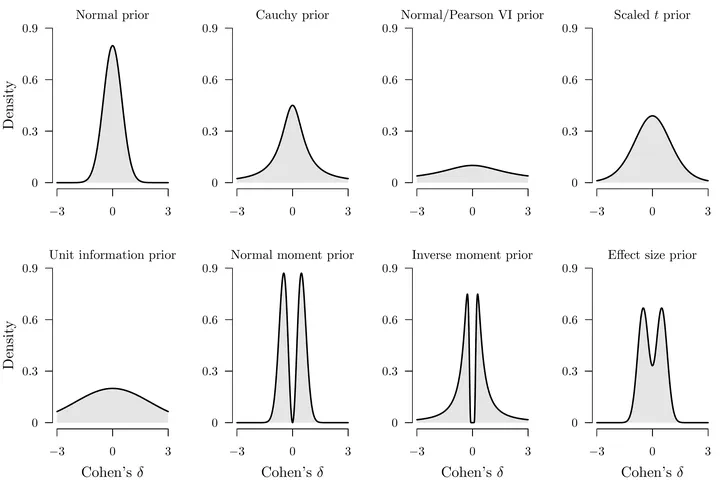
In this paper we focus on null hypothesis Bayesian testing and the so-called Bayes factor for the independent samples $t$-test. The JZS Bayes factor (Rouder et al., 2009) is currently the de-facto default in popular software currently in use. This Bayes factor is based on setting a Cauchy prior on the standardized effect size $\delta$. In this paper we introduce the prior predictive paradox: JZS Bayes factors may support the alternative model that $\delta$ is not zero, while at the same time the supported model may generate much more unreasonable data than the seemingly worse null hypothesis that $\delta=0$. This paradox may appear to be in direct conflict with the very definition of the Bayes factor and therefore must be addressed. We explain how this paradox can arise, why it matters, and we offer an alternative approach that avoids the problem altogether. We further question the choice of the default prior for the test at hand by comparing its performance with seven other priors.